Knowing the hours of sunset and sunrise may be handy in a variety of situations, an automated chicken coop door might be only one example.
There are several ways to get the proper times: a lookup table in EEPROM, the Timelord library or one of its successors, the Dusk2Dawn library, a rather complicated calculation including the Julian calender, or a fairly simple approximation that I will discuss here.
This method uses the average of the earliest and latest sunset and then for any given day adds or subtracts a certain amount of time with a maximum of half of the difference between the earliest and latest sunrise.
Rob Tillaert discusses the method here. It presumes that the sunrise time follows a (co)sinoidal function. I will try to visualize it with a simple example:
Say that on June 23 the earliest sunrise of the year occurs at 4am, and that the latest sunrise of the year occurs at 23 December at 6 am.
Then you know that on any other day the sunrise is between 4 and 6 am. If you take the average that is 5 am, then you know that every other sunrise that year is either 0-1 hr later than 5 am or 0-1 hr earlier than 5 am.
It is the latter that is captured in the formula:
t=avg+0.5Δ*cos((doy+8)/58.09)
- avg is average sunrise time, in minutes since midnight
- Δ the difference between the earliest and latest sunrise time
- doy is the day of the year
- the 8 is there because we start on the wintersolstice: 23 December is 8 days before jan 1
- 58.09 is 365/2π. That is necessary because the cosinusfunction has max 2π as input.
If you live in a DST zone, the earliest sunrise wil be under DST, however you need the non-DST corrected time: the sun knows no DST. Calculate firstm then add DST later
For my location the earliest and latest sunrise are:
earliest sunrise is at 4.19 am
latest sunrise is at 8.51
in order to use them in our equation, we have to calculate them in minutes past midnight:
4.19= 4×60+19=259
8.51= 8*60+51=531
The average is (259+531)/2=395
the difference or delta is 531-259=272. We need half of that which is 137.
The equation then becomes:
395+137*cos((doy+8)/58.09)
To check the accuracy of the approximation, I plotted the actual sunrise times (blue curve) against the calculated sunrise time (red curve).
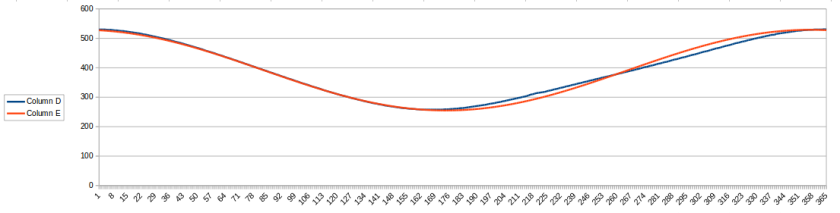As it shows, the first half of the year is a perfect fit, the second half of the year seems to follow a more linear curve with the max deviation being 20 minutes, that may or may not be accurate enough for your project. With the aid of this curve though I could opt for a linear approximation for the 2nd half of the year.
For sunset we can practically use the same formula, be it that we now have to subtract the variable part rather than add it.
For my location the sunset is as follows:
latest: 22:07 =1327
Earliest: 16:27= 987
avg=2287/2=1144
delta=1327-987=340 ->170
sunset=1144-170*cos((doy+8)/58.09)
That gives the following graph:
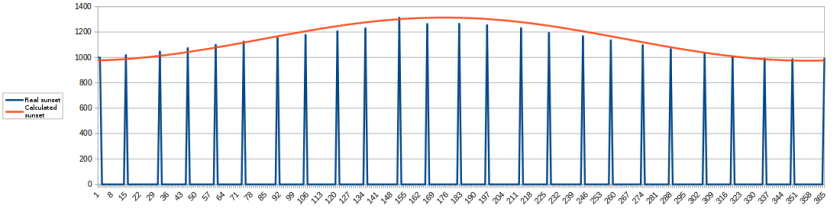This time I didnt bother to enter all the real sunset times, but it is clearly visible that there is a reasonable fit that could maybe be enhanced a bit by shifting it slightly more to left or decreasing the delta a bit. Again Red graph is the calculated sunset, the blue is the actual sunset. None of the graphs has been corrected for DST.
A procedure for the Arduino would look as follows:
Where DST is a byte indicating whether DST is active (1) or not active (0).
The day of the year I pull from my RTC library but it can also be calculated as follows:
int(((month-1)*30.5)+dayOfMonth) (that is an approximation though)
The sunrise and sunset are both given in minutes after midnight. The hour and minutes of the sunrise (and sunset) can be calculated by:
hour=sunrise/60
minute=sunrise%60
Arduino, ESP8266, ESP32 & Raspberry Pi stuff 
Cool stuff and certainly enough for the chickens. Alternatively, you can use my star pointer code http://www.instructables.com/id/Two-Axis-Star-Tracker/ , strip it down to the sun only, of course remove all the motor stuff and use Altitude. You always need a RTC of course. If you fetch the time from the internet, I think there are services to get sunrise and/or altitude online.
As a matter of fact I was thinking about your startracker when writing this, promising myself I have to dive deeper in that code.
Indeed, still need an RTC, not for the calculation but to do anything useful with the found times.
Pulling time from an NTP server (if connection to internet) is an option…. but as you say might as well pull the sunrise sundown as well.
So this is mainly for selfsustained systems that have an RTC.
usually the question comes up: “why not just an LDR?” but there are drawbacks to that, mainly that the project then needs access to the outside (not everything is a chicken coop) but also the difference between dawn and a very dark sky can be difficult and it becomes a bit harder to plan activities say ‘one hour before sunrise’ (although you could store the sunrise from the day before)
Hi and my apologies for reporting your hemispheral raciaism…. (:-)> If I am in the southern hemisphere is there a sin type function that will give the inverse result? – If so i didnt find it – the best i could do is a n – cos(… which depends on the difference.
Alastair, thanks, I escaped hemespherism prosecution. I didn’t specifically try this for the southern hemisphere, never realised it would be different there as the principle applies to both half of the globe: there is an earliest and latest moment the sun rises or sets and any other sunrise or sunset should move between those. My function is an approximation but as you can see, at some point even a linear function would have been better. The only difference I see is that the peaks must have shifted by 1pi (180 degrees)
In the sample procedure code provided above (“A procedure for the Arduino would look as follows:”), 60 minutes is subtracted when DST =1 (when DST is in effect). I was wondering if 60 minutes should actually be added, not subtracted during DST. I hesitate to ask because this page has been published for several years and no one else has mentioned it – so I could easily be wrong. Except that I only get the correct times for sunrise and sunset when I add 60 minutes during DST.
Thanks for the great simplified approximation for calculating sunrise and sunset times. It’s very useful.
The fact that it has been up for several years with no one questioning it doesn’t guarantee it is correct. I am hesitant to just plainly say add or subtract an hour coz that easily leads to mistakes so let’s see where there might be a problem.
The formula for sunrise calculates for regular uncorrected time. So say at a date in summer it may tell you the sunrise is at 6 a.m. uncorrected time. In summertime the clock has been put forward 1 hour, so when that sunrise happens at 6, your clock already says 7, so it seems you are right