Calculating Sunrise and Sunset on Arduino (or other microcontroller)

Knowing the hours of sunset and sunrise may be handy in a variety of situations, an automated chicken coop door might be only one example.

There are several ways to get the proper times: a lookup table in EEPROM, the Timelord library or one of its successors, the Dusk2Dawn library, a rather complicated calculation including the Julian calender, or a fairly simple approximation that I will discuss here.

This method uses the average of the earliest and latest sunset and then for any given day  adds or subtracts a certain amount of time with a maximum of half  of the difference between the earliest and latest sunrise.

Rob Tillaert discusses the method here. It presumes that the sunrise time follows a (co)sinoidal function. I will try to visualize it with a simple example:

Say that on June 23 the earliest sunrise of the year occurs at 4am, and that the latest sunrise of the year occurs at 23 December at 6 am.

Then you know that on any other day the sunrise is between 4 and 6 am. If you take the average that is 5 am, then you know that every other sunrise that year is either 0-1 hr later than 5 am or 0-1 hr earlier than 5 am.

It is the latter that is captured in the formula:

t=avg+0.5Δ*cos((doy+8)/58.09)

• avg is average sunrise time, in minutes since midnight
• Δ the difference between the earliest and latest sunrise time
• doy is the day of the year
• the 8 is there because we start on the wintersolstice: 23 December is 8 days before jan 1
• 58.09 is 365/2π. That is necessary because the cosinusfunction has max 2π as input.

If you live in a DST zone, the earliest sunrise wil be under DST, however you need the non-DST corrected time: the sun knows no DST. Calculate firstm then add DST later

For my location the earliest and latest sunrise are:

earliest sunrise is at 4.19 am
latest sunrise is at 8.51
in order to use them in our equation, we have to calculate them in minutes past midnight:
4.19= 4×60+19=259
8.51= 8*60+51=531
The average is (259+531)/2=395
the difference or delta is 531-259=272. We need half of that which is 137.
The equation then becomes:

395+137*cos((doy+8)/58.09)

To check the accuracy of the approximation, I plotted the actual sunrise times (blue curve) against the calculated sunrise time (red curve).

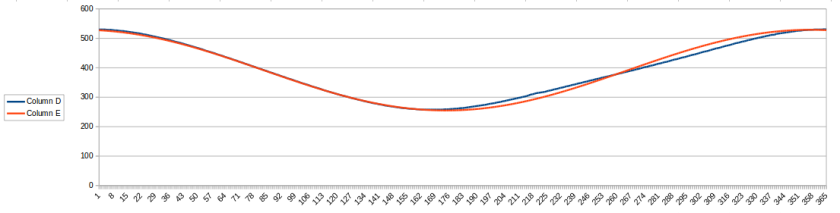As it shows, the first half of the year is a perfect fit, the second half of the year seems to follow a more linear curve with the max deviation being 20 minutes, that may or may not be accurate enough for your project. With the aid of this curve though I could opt for a linear approximation for the 2nd half of the year.

For sunset we can practically use the same formula, be it that we now have to subtract the variable part rather than add it.
For my location the sunset is as follows:
latest: 22:07 =1327
Earliest: 16:27= 987
avg=2287/2=1144
delta=1327-987=340 ->170
sunset=1144-170*cos((doy+8)/58.09)

That gives the following graph:

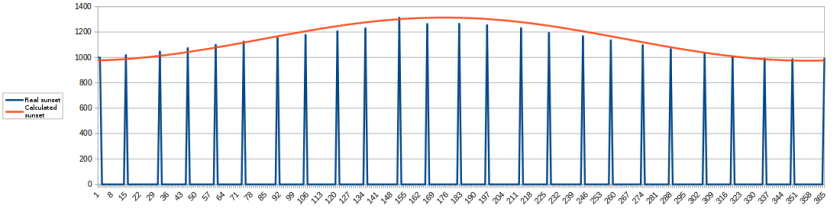This time I didnt bother to enter all the  real sunset times, but it is clearly visible that there is a reasonable fit that could maybe be enhanced a bit by shifting it slightly more to left or decreasing the delta a bit. Again Red graph is the calculated sunset, the blue is the actual sunset. None of the graphs has been corrected for DST.

A procedure for the Arduino would look as follows:
Where DST is a byte indicating whether DST is active (1)  or not active (0).
The day of the year I pull from my RTC library but it can also be calculated as follows:
int(((month-1)*30.5)+dayOfMonth)  (that is an approximation though)

The sunrise and sunset are both given in minutes after midnight. The hour and minutes of the sunrise (and sunset) can be calculated by:
hour=sunrise/60
minute=sunrise%60