Measuring temperature with NTC-The Steinhart-Hart Formula

I know, this subject can be found all over the web, but the calculations sometimes are   presented a bit cryptic as if the author  wanted to put as many nested calculations on one line, so I just wanted to write something that explains it step by step, especially where the actual calculations are concerned. Lady Ada does a good job explaining the use of the thermistor, but I added some more explicit calculations.
The Arduino has several ADC ports that we can use to read a voltage, or rather an ‘ADC value’. If the Analog port is connected to Vcc, the max value one  reads is 1023 and of course when connected to ground it is 0.
Now if we make a voltage divider which is typically two resistors in series between Vcc and Ground and the analogport in the middle, the reading will depend on the ratio of the two resistors: If they are equal, the reading will be 512, halfway to 1023. If one of the resistors, say the bottom one is an NTC, then the readings on the analogport will vary with the temperature:
If the temperature goes down, the value of the resistor increases and so will the reading on the analog port.

Suppose we have a 10k Seriesresistor and an NTC that for now we call ‘R’.
Then the voltage that can be measured in the middle is

Vo=R/(R+10K) * Vcc

The analogPort readings however don’t give a voltage but an ADC value that can easily be calculated
ADC value= Vo*1023/Vcc  // if for instance the Vo=4Volt the ADC = 818
or
ADC value= 1023 *(Vo/Vcc)

If we now combining the two formulas or as it is called ‘substitute’ Vo in the formula for ADC we get the following:
ADC value= (R/(R+10K))*Vcc*1023/Vcc
As we multiply by Vcc but also divide by Vcc we can take that out of the equation and end up with
ADC value= (R/(R+10k))*1023
ADC value=  1023*R/(10+R)
if we want to get the value of R out of that equation, that becomes
R=10k/(1023/ADC-1)
If that goes a bit too fast, here is the equation worked out. I prefer pictures over the ‘in line’ formulas as some people have problems understanding the PEMDAS / BODMAS order of operation.

This becomes

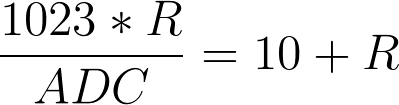
subtraction of R
Work  -R into the multiplication
As we are interested in R, divide both sides by the enclosed fracture

The ’10’ stood for ’10k’
and as we don’t always use a 10k we just make it more general:
So, as long as we know the value of the series resistor, we can calculate the value of the NTC from the measured ADC value. Now remember, this is valid voor a pull-up configuration. If it is a pull down configuration, the calculation of the ADC to resistor value is  the inverse.

R_ntc = R_series*(1023/ADC-1);// for pull down
R_ntc = R_series/(1023/ADC – 1)); // for pull-up configuration

So what would that look like in a  program?

//Measure NTC value
byte NTCPin = A0;
const int SERIESRESISTOR = 10000;
void setup()
{
	Serial.begin(9600);
}
void loop()
{
	float ADCvalue;
	float Resistance;
	ADCvalue = analogRead(NTCPin);
	Serial.print("Analog value ");
	Serial.print(ADCvalue);
	Serial.print(" = ");
//convert value to resistance
	Resistance = (1023 / ADCvalue) - 1;
	Resistance = SERIESRESISTOR / Resistance;
	Serial.print(Resistance);
	Serial.println(" Ohm");
	delay(1000);
}
//end program

Knowing the resistance of the NTC is nice but it doesn’t tell us much about the temperature… or does it?
Well many NTC’s have a nominal value that is measured at 25 degrees Centigrade, so if you have a 10k NTC and you measure it to be 10k, that means it is 25 degrees at that moment. That doesn’t help you much when the measurement is different.
You could keep a table in which every resistance value stands for a temperature. Those tables are very accurate but require a lot of work and memory space.

However, there is a formula, the Steinhart-Hart equation, that does a good approximation of converting resistance values of an NTC to temperature. Its not as exact as the thermistor table ( after all it is an approximation) but its fairly accurate.

The Steinhart-Hart equation looks like this:
That is a rather complex equation that requires several parameters (A, B, C) that we normally do not have for the run of the mill NTC.There are two things we can do. We can take 3 readings with a calibrated temperature and then work out the A, B and C parameters.

but fortunately there is a simplification of this formula, called the B-parameter Equation. That one looks as follows:
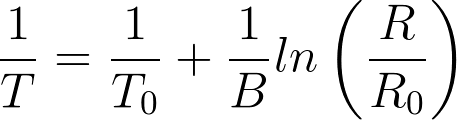To is the nominal temperature, 25 °C in Kelvin (= 298.15 K). B is the coefficient of the thermistor (3950 is a common value). Ro is the nominal resistance of the NTC  (thus at 25 degrees). Let’s say we have a 10Kohm NTC. We only need to plug in R (the resistance measured) to get T (temperature in Kelvin) which we then convert to °C.

The program looks as follows:

//---------------
byte NTCPin = A0;
#define SERIESRESISTOR 10000
#define NOMINAL_RESISTANCE 10000
#define NOMINAL_TEMPERATURE 25
#define BCOEFFICIENT 3950

void setup()
{
Serial.begin(9600);
}
void loop()
{
float ADCvalue;
float Resistance;
ADCvalue = analogRead(NTCPin);
Serial.print("Analog value ");
Serial.print(ADCvalue);
Serial.print(" = ");
//convert value to resistance
Resistance = (1023 / ADCvalue) - 1;
Resistance = SERIESRESISTOR / Resistance;
Serial.print(Resistance);
Serial.println(" Ohm");

float steinhart;
steinhart = Resistance / NOMINAL_RESISTANCE; // (R/Ro)
steinhart = log(steinhart); // ln(R/Ro)
steinhart /= BCOEFFICIENT; // 1/B * ln(R/Ro)
steinhart += 1.0 / (NOMINAL_TEMPERATURE + 273.15); // + (1/To)
steinhart = 1.0 / steinhart; // Invert
steinhart -= 273.15; // convert to C

Serial.print("Temperature ");
Serial.print(steinhart);
Serial.println(" oC");
delay(1000);
}
//-------------

This ofcourse is not an ideal program. It is always good to take a few samples and to average them.
The following function can do that for you:

float sample(byte z)
/* This function will read the Pin 'z' 5 times and take an average.
 */
{
	byte i;
	float sval = 0;
	for (i = 0; i < 5; i++)
	{
	sval = sval + analogRead(z);// sensor on analog pin 'z'
	}
	sval = sval / 5.0;    // average
	return sval;
}

Feeding the series resistor and NTC from the 5 Volt supply from the Arduino is possible. The Arduino power line does have glitches though. For accurate measurements it is better to use the 3.3Volt line as analog reference and feed the resistor from there.
for that add the following code in the setup
// connect AREF to 3.3V and use that as VCC for the resistor and NTC!
analogReference(EXTERNAL);